Historischer Redoxbegriff
Früher verstand man unter einer Oxidation generell eine Reaktion mit Sauerstoff, wie z.B. das Verbrennen von Magnesium an der Luft oder im reinen Sauerstoff. Es kommt zu einem grellen Leuchten entsteht das weiße Magnesiumoxid.
$$ \ce{Mg(s) + O2(g) -> MgO(s)}$$
Früher verstand man unter einer Reduktion immer das Entfernen von Sauerstoff aus einer Verbindung. So wird z.B. beim Erhitzen von Quecksilber(II)-oxid Sauerstoff frei.
$$ \ce{ 2 HgO(s) -> 2 Hg(s) + O2(g) } $$
Heutiger Redoxbegriff
Wird z.B. in einem Standzylinder Bromgas gefüllt, also kein Sauerstoff vorhanden ist, und wird dann ein brennender Magnesiumspan hineingebracht, kommt es ebenfalls zu einem hellen Leuchten und es entsteht weiterhin ein farbloses Pulver, das gut in Wasser löslich ist.
Dieses Pulver ist Magnesiumbromid.
$$ \ce{Mg (s) + Br_2 (g) -> MgBr_2 (s) } $$
Oxidationen und Reduktionen finden also auch gänzlich ohne Sauerstoff statt und werden jetzt auf der Grundlage von Elektronenbewegungen definiert.
Oxidation: Abgabe von Elektronen
Reduktion: Aufnahme von Elektronen
Redoxreaktion (Reduktions-Oxidations-Reaktion): Reaktion mit Elektronenübergängen
Oxidationsmittel: Teilchen, die als Elektronenakzeptor wirken, weil sie den Reaktionspartner oxidieren. Es selbst wird reduziert,
Reduktionsmittel: Teilchen, die als Elektronendonator wirken, weil sie den Reaktionspartner reduzieren. Es wird oxidiert. Betrachten wir unser Beispiel mit dem Magnesium. Magnesiumatome reagieren mit Sauerstoffmolekülen zu Magnesiumoxid, das aus Magnesiumionen und Oxidionen besteht.
Die Magnesiumatome geben jeweils zwei Elektronen ab.
Auch bei der Reaktion mit Brom findet eine Redoxreaktion statt. Magnesiumatome geben jeweils zwei Elektronen ab, werden also oxidiert. Bei den Brommolekülen nimmt jeweils ein Elektron aufgenommen und es entstehen Bromidionen. Brom wird reduziert.
$$ \ce{\overset{0}{Mg} + \overset{0}{Br}_2 -> \overset{+II}{Mg}^{2+} + 2 \overset{-I}{Br^-}}$$
Oxidationszahlen
Bei den oben gezeigten Reaktionsgleichungen wurden bei den Teilchen Zahlen angegeben, die als Oxidationszahlen bezeichnet werden.
Wenn sich die Oxidationszahlen von den Edukten zu den Produkten nicht ändern, liegt auch keine Redoxreaktion vor. Wird die Oxidationszahl positiver, handelt es sich um eine Oxidation und wenn die Oxidationszahl negativer wird um eine Reduktion.
In den nächsten Kapiteln werden wir lernen, wie Oxidationszahlen bestimmt werden. Mit dem Begriff der Oxidationszahl wird der bekannte Begriff von der Wertigkeit erweitert. Die Wertigkeit gibt an, wieviele einwertige Atome (z.B. H+ oder Cl–) an ein Element gebunden werden können. So ist Magnesium zweiwertig, denn es wird MgCl2 gebildet.
Wie ist das mit der gedachten Ladung gemeint?
Schauen wir uns die Reaktionsgleichung für die Bildung von Wasser aus den Elementen an.
$$ \ce{ 2 H2 + O2 -> 2 H2O} $$
Alle beteiligten Teilchen sind Moleküle, weshalb keine formalen (ganzen) Ladungen vorliegen können. Daher gehen wir z.B. beim Wasser davon aus, dass es aus den Atomionen Wasserstoffionen H+ und Oxidionen O2- besteht.
Bestimmung der Oxidationszahlen mit den Lewis-Formeln
Wie der name schon sagt, geht man bei dieser Methode von der Lewis-Formel aus, also der Strukturformel mit allen bindenden und nichtbindenden Elektronenpaaren. Für ein Elektronenpaar kann hier selbstverständlich auch ein Strich benutzt werden.
Als nächstes benötigen wir eine besonders simple Formel:
$$OZ = VZ – EZ$$
Hierbei ist OZ die Oxidationszahl, VZ die Valenzelektronenzahl (Außenelektronen) und EZ die zugeordnete Elektronenzahl. Sehen wir uns das am Beispiel Wasser an. Zunächst zeichnen wir die korrekte Lewisformel. Sauerstoff ist in der VI. Hauptgruppe, verfügt demnach über sechs Außenelektronen. Zwei Elektronen werden für die Atombindungen zu den beiden Wasserstoffatomen benötigt. Es verbleiben freie Elektronen, also zwei freie Elektronenpaare.
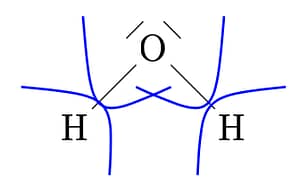
Jetzt gehen wir nach einem Prinzip vor, das ich immer das ABBA-Prinzip nenne: The Winner Takes It All, also der Gewinner kriegt alles. Gemeint ist hierbei, dass das Bindungsatom mit der höchsten Elektronegativität (EN) das komplette Elektronenpaar zugesprochen bekommt. Demnach zeichnen wir die Halbkreise ein. $$
\begin{align*}
EN(H) & = 2,1 \\
EN(O) & = 3,5\\
\end{align*}
$$
Wie leicht zu sehen ist, besitzt Sauerstoff eine höhere Elektronegativität als Wasserstoff. Damit bekommt Sauerstoff die beiden bindenden Elektronenpaare zum Wasserstoff zugeschlagen. Die zugeordnete Elektronenzahl für Sauerstoff ist 8 (4 Elektronenpaare innerhalb der Halbkreise) und für Wasserstoff ist EZ=0.
Mit den Valenzelelektronenzahlen von Sauerstoff und Wasserstoff, nämlich 6 und 1, können wir die Oxidationszahlen berechnen. Diese geben wir, mit Ausnahme der Null, in römischen Ziffern an.
$$
\begin{align*}
OZ &= VZ – EZ \\
OZ(O) &= 6 – 8 = -II \\
OZ(H) &= 1 – 0 = +I
\end{align*}
$$
Die Oxidationszahlen werden über die jeweiligen Atome notiert.
Jetzt wollen wir uns mit Alkohol beschäftigen, genauer gesagt mit Ethanol. Hier taucht das Element Kohlenstoff auf mit EN(C)=2,5. Damit ergeben sich die folgenden Elektronenzuordnungen, denn Kohlenstoff gewinnt gegen Wasserstoff und Sauerstoff gegen Kohlenstoff und Wasserstoff. Zwischen den beiden Kohlenstoffatomen werden die beiden Elektronen aufgeteilt, da hier selbstverständlich die Elektronegativitäten gleich sind. Kohlenstoff steht in der IV. Hauptgruppe, verfügt demnach über vier Valenzelektronen. Für alle Wasserstoffatome ergeben sich die gleichen Ordnungszahlen. Für die beiden Kohlenstoffatome müssen die Oxidationszahlen berechnet werden.

Für alle Wasserstoffatome ergeben sich die gleichen Ordnungszahlen. Für die beiden Kohlenstoffatome müssen die Oxidationszahlen berechnet werden.
$$
\begin{align*}
OZ &= VZ – EZ \\
OZ(O) &= 6 – 8 = -II \\
OZ(H) &= 1 – 0 = +I \\
OZ(C_1) &= 4 – 5 = -I \\
OZ(C_2) &= 4 – 7 = -III\\
\end{align*}
$$
Die Oxidationszahlen schreiben wir über die betreffenden Atome.
Bestimmung der Oxidationszahlen nach den Regeln
Die Regeln für das Aufstellen der Oxidationszahlen lauten wie folgt:
- Die Summe der Oxidationszahlen aller Atome Verbindung ist so groß wie die Ladung der Verbindung.
- Elemente in ihrer stabilen Form bekommen die Oxidationszahl 0 . Hier ist die BrINClHOF-Regel zu beachten, gemäß der die Elemente Brom, Iod, Stickstoff, Chlor, Wasserstoff, Sauerstoff und Fluor stabile zweiatomige Moleküle bilden.
$$
\ce{ \overset{0}{Mg} \quad \overset{0}{Hg} \quad \overset{0}{H_2} \quad \overset{0}{F_2} \quad \overset{0}{He} }
$$ - Bei einatomigen Ionen entspricht die Oxidationszahl der Ladung:
$$
\ce{ \overset{I}{Na^+} \quad \overset{II}{Cu^{2+}} \quad \overset{III}{Al^{3+}} \quad \overset{-I}{Cl^-} }
$$ - Bei mehratomigen Ionen entspricht die Summe der Oxidationszahlen der Ladung:
$$
\ce{ \overset{IV}{S}\overset{-II}{O_3^{2-}} \quad \overset{VI}{S} \overset{-II}{O_4^{2-}} \quad \overset{V}{P}\overset{-II}{O_4^{3-}} }
$$ - In Verbindungen hat Fluor die Oxidationszahl -I (es hat die höchste Elektronegativität im Periodensystem):
$$
\ce{ Na\overset{-I}{F} \quad Al\overset{-I}{F_3} \quad H\overset{-I}{F} \quad Ca\overset{-I}{F_2} }
$$ - In Verbindungen hat Wasserstoff die Oxidationszahl +I, außer in Metallhydriden (Verbindungen von Metallen mit Wasserstoff) -I:
$$
\ce{ \overset{+I}{H_2}O \quad \overset{+I}{H}F \quad Na\overset{-I}{H} \quad Ca\overset{-I}{H_2} }
$$ - In Verbindungen hat Sauerstoff die Oxidationszahl -II, außer in Peroxiden (Verbindung O mit O, z.B. Wasserstoffperoxid) -I:
$$
\ce{ H_2\overset{-II}{O} \quad CaC\overset{-II}{O_3} \quad Mg\overset{-II}{O} \quad H_2\overset{-I}{O_2} }
$$
Redoxreaktionen in fester Phase
Versuch: Reaktion vom Kupfer(II)-oxid mit Kohlenstoff
In einem Reagenzglas, das annähernd senkrecht eingespannt worden ist, wird ein Gemisch aus schwarzem Kupferoxid und Kohlenstoff erhitzt, bis das Gemisch zu glühen anfängt.
Das Gemisch brennt selbständig durch. Im Gemisch sind rötliche Spuren erkennbar.Deutung
Es entsteht metallisches Kupfer in einer exothermen Redoxreaktion.
Berechnen Sie, welche Masse an Kohlenstoff für die Reaktion von 2,0g Kupferoxid benötigt wird. $$
\begin{align*}
\frac{n(CuO)}{n(C)} &= \frac{2}{1} \\
n(C) &= \frac{n(CuO)}{2}\\
&= \frac{m(CuO)}{M(CuO) \cdot 2 } \\
& = \frac{2g}{79,5g/mol \cdot 2} \\
& = 0,01257mol \\
m(C) &= n(C) \cdot M(C) \\
&= 0,01257mol \cdot 12g/mol \\
&= \underline{0,151g}
\end{align*}
$$
Versuch: Reaktion vom Kupfer(II)-oxid mit Eisen
In einem Reagenzglas, das annähernd senkrecht eingespannt worden ist, wird ein Gemisch aus schwarzem Kupferoxid und Eisenpulver erhitzt, bis das Gemisch zu glühen anfängt.
Das Gemisch brennt selbständig durch. Im Gemisch sind rötliche Spuren erkennbar.
Es entsteht metallisches Kupfer in einer exothermen Redoxreaktion.
$$
\ce{Fe (s) + CuO (s) -> FeO (s) + Cu (s) }
$$
Teilgleichungen für die Oxidation und die Reduktion unter Angabe der relevanten Oxidationszahlen:
$$
\begin{align*}
\text{Ox: } & \ce{ \overset{0}{Fe} -> \overset{+II}{Fe}^{2+} + 2 e- } \\
\text{Red: } & \ce{ \overset{II}{Cu}^{2+} + 2e- -> \overset{0}{Cu} } \\
\text{Redox: } & \ce{Fe + Cu^{2+} -> Fe^{2+} + Cu}
\end{align*}
$$
Berechnen Sie, welche Masse Eisen eingesetzt werden muss, damit 1 g Kupferoxid stöchiometrisch umgesetzt wird.
$$
\begin{align*}
\frac{n(Fe)}{n(CuO} &= \frac{1}{1}\\
n(Fe) &= n(CuO) \\
n(CuO) &= \frac{m(CuO}{M(CuO}\\
&= \frac{m(CuO)}{M(CuO)} \\
&= \frac{1g}{79,5g/mol}\\
&= 0,01258mol \\
n(Fe) &= 0,01258mol \\
m(Fe) &= n(Fe) \cdot M(Fe)\\
&= 0,01258mol \cdot 56g/mol \\
&= \underline{0,7045g}
\end{align*}
$$
Aluminothermie
Dieses Verfahren, das auch als Thermitverfahren bekannt ist, wurde von Hans Goldschmidt 1895 zum Patent angemeldet. Hierbei wird die starke Reaktivität des Aluminiums gegenüber Sauerstoff genutzt, Eisenoxid wird zu Eisen reduziert. Letzteres ergibt sich aus der Redoxreihe der Metalle. Die Reaktion ist stark exotherm und es entstehen Temperaturen um 2000°C.
Das Thermitverfahren wird im Gleisbau genutzt. Die beiden Schienenenden werden mit dem entstehenden flüssigen Eisen verschweißt.
Auf der Grundlage des Thermitverfahrens wurden in den 1930er Jahren Brandbomben (Elektron-Thermit-Stabbrandbomben) in Großbritannien und Deutschland entwickelt, die von beiden Seiten im 2. Weltkrieg eingesetzt worden sind. In Dresden kamen während eines Angriffs allein 650 Tausend derartiger Brandbomben zum Einsatz.
Wir können hierzu einen Versuch durchführen:
Versuch: Reaktion von Aluminium mit Eisenoxid
Ein Thermitgemisch aus 20 g Eisen(III)-oxid und 7 g Aluminium wird hergestellt.
Der Wasserablauf eines eingespannten Blumentopfs wird mit einer Aluminiumfolie verschlossen und darauf ein Papprohr mit einem Durchmesser von 1 bis 2 cm gestellt. Der Blumentopf wird um das Papprohr herum mit Sand gefüllt.
Das Thermitgemisch wird in die Pappröhre gegeben. Unter den Blumentopf wird ein feuerfestes Gefäß mit Sand gestellt.
Das Thermitgemisch wird mit einer brennenden Wunderkerze gezündet.
Aus der Öffnung des Blumentopfes tropft flüssiges Metall.
Deutung
$$
\ce{Fe2O3 + 2 Al -> 2 Fe + Al2O3}
$$
Es findet eine Redoxreaktion statt. Eisen(III)-oxid wird durch Aluminium zu Eisen reduziert, Aluminium wird zu Aluminiumoxid oxidiert.
$$
\begin{align*}
\text{Ox: } & \ce{ \overset{0}{Al} -> \overset{+III}{Al}^{3+} + 3 e- } \\
\text{Red: } & \ce{ \overset{III}{Fe}^{3+} + 3e- -> \overset{0}{Fe} } \\
\text{Redox: } & \ce{Al + Fe^{3+} -> Fe + Al^{3+} }
\end{align*}
$$
Der Hochofenprozess
Als Ausgangsstoffe in einem Hochofen dienen Koks, Zuschläge, Erz und Luft. Die Zuschläge reagieren mit der Gangart (Begleitgestein des Eisenerzes) zu Schlacke. Reaktionsprodukte sind das Gichtgas, die Schlacke und natürlich das Roheisen. Gichtgas besteht Stickstoff, Kohlenstoffmonoxid, Kohlenstoffdioxid und Wasserstoff.
Das wichtigste Reduktionsmittel im Hochofen ist Kohlenstoffmonoxid. Es entsteht durch die Verbrennung von Koks mit der eingeblasenen vorgewärmten Luft und die anschließende Reaktion des entstandenen Kohlenstoffdioxids mit Kohlenstoff.
Bei der zuletzt genannten Reaktion handelt es sich um eine Gleichgewichtsreaktion (Bouduard-Gleichgewicht). Die Verbrennung des Kohlenstoffs zu Kohlenstoffdioxid ist stark exotherm und liefert die Energie für den Hochofenprozess.
$$
\ce{ \overset{0}{C} + \overset{0}{O2} -> \overset{IV}{C}\overset{-II}{O2} }
$$
Kohlenstoffdioxid reagiert weiter zu CO.
$$
\ce{ \overset{IV}{C}\overset{-II}{O2} + \overset{0}{C} <=> 2 \overset{II}{C}\overset{-II}{O} }
$$
Durch das Kohlenstoffmonoxid wird der Roteisenstein (Fe2O3) in das stärker eisenhaltige Magnetit (Magneteisenstein, Fe3O4) überführt (1). Magnetit reagiert weiter reduziert zu Eisen(II)-oxid, das wiederum in (3) reduziert wird zu Eisen, das sich im Hochofen sammelt.
$$
\begin{align*}
(1) & \ce{Fe2O3 + CO -> 2 Fe3O4 + CO2 } \\
(2) & \ce{Fe3O4 + CO -> 3 FeO + CO2 } \\
(3) & \ce{FeO + CO -> Fe + CO2 }\\
(1+2+3) & \ce{ 3 \overset{II}{C}O + \overset{III}{Fe2}O3 -> 3 \overset{IV}{C}O2 +2 \overset{0}{Fe} }
\end{align*}
$$
Bestimmt man die Oxidationszahlen vom Fe3O4, wird man sehr bald auf ein Problem stoßen. Eisen hat in der Formel die Oxidationszahl 2,67. Das liegt an der irreführenden Formel. Magnetit ist eigentlich FeO ⋅ Fe2O3 mit den Oxidationszahlen für Eisen von +II und +III und eine Formel kann präziser und weniger irreführend mit Fe2+(Fe3+)2O4 formuliert werden.
Wie man in der zusammenfassenden Gleichung (1+2+3) sieht, ändert sich die Oxidationszahl beim Kohlenstoff von +II nach +IV. Demnach findet hier eine Oxidation statt und beim Eisen eine Reduktion (von +III nach 0).
Reaktion einer Kaliumpermanganatlöung mit Salzsäure
Im Abzug lässt man konzentrierte Salzsäure auf eine konzentrierte Kaliumpermanganatlösung einwirken.
Die Lösung entfärbt sich. Es ist ein Chlorgeruch wahrnehmbar.
Chlorid-Ionen werden zu gasförmigem Chlor oxidiert (die Oxidationszahl des Chlor steigt von -I auf 0) und Permanganationen werden werden zu Mangan(II)-Ionen oxidiert (die Oxidationszahl fällt von VII auf II).
Weierhin kann hier, da wir eine saure Lösung vorliegen haben, mit H+-Ionen und H2O ausgeglichen werden.
$$
\begin{align*}
\text{Ox: } & \ce{2 \overset{-I}{Cl^-} -> \overset{0}{Cl_2} + 2e- } \\
\text{Red: } & \ce{ \overset{VII}{\ce{Mn}}O4- + 5e- + 8 H+ -> \overset{II}{Mn^{2+}} + 4 H2O } \\
\text{Redox: } & \ce{ 10 Cl- + 2 MnO4- + 10e- + 16 H+ -> 5 Cl2 + 10e- + 2 Mn^{2+} + 8 H2O} \\
& \ce{ 10 Cl- + 2 MnO4- 16 H+ -> 5 Cl2 + 2 Mn^{2+} + 8 H2O}
\end{align*}
$$
Reaktion von Permanganat-Ionen mit Eisen(II)-Ionen in saurer Lösung
5 ml Kaliumpermanganat-Lösung werden mit Schwefelsäure angesäuert und mit frischer Eisen(II)-sulfat-Lösung versetzt
Die Lösung färbt sich braun.
Es sind braune Eisen(III)-ionen entstanden. Die Oxidationszahl von Eisen verändert sich von +II nach +III. Demnach liegt eine Oxidation vor. Beim Mangan hingegen ist eine Reduktion zu verzeichnen, da die Oxidationszahl von +VII nach +II negativer wird.
Weierhin kann hier, da wir eine saure Lösung vorliegen haben, mit H+-Ionen und H2O ausgeglichen werden.
$$
\begin{align*}
\text{Ox: } & \ce{\overset{II}{Fe^{2+}} -> \overset{III}{Fe^{3+}} + e- } \\
\text{Red.: } & \ce{ \overset{VII}{\ce{Mn}}O4- + 5e- + 8 H+ -> \overset{II}{Mn^{2+}} + 4 H2O } \\
\text{Redox: } & \ce{ 5 Fe^{2+} + MnO4- + 5e- + 8H+ -> 5 Fe^{3+} + 5e- + Mn^{2+} + 4H2O} \\
& \ce{ 5 Fe^{2+} + MnO4- + 8H+ -> 5 Fe^{3+} + Mn^{2+} + 4H2O}
\end{align*}
$$